Mathématiques et Sciences sociales

Les mathématiques apportent peu aux Sciences sociales ; elles ne font, en général, que quantifier des trivialités. Nous savons que les sciences progressent souvent quand l’inattendu arrive et le dilemme du prisonnier ¹ est un de ces cas miraculeux où les mathématiques apportent un éclairage nouveau sur notre comportement social. Ce domaine a été renouvelé récemment par un article fracassant de Freeman Dyson et William Press [1].

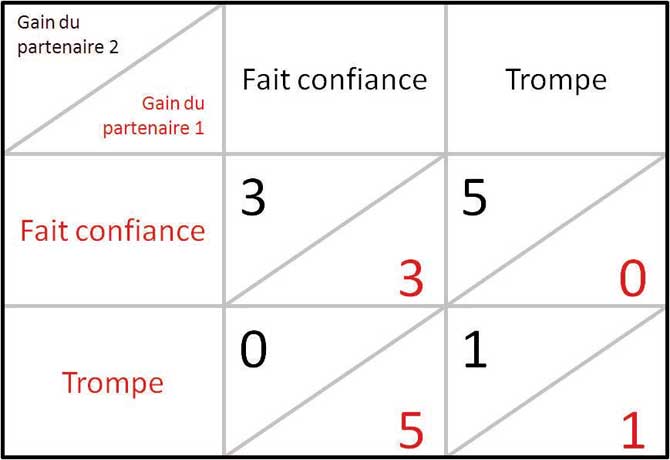
Le point de départ est une situation de « duel », c’est-à-dire une partie entre deux personnes ; dans la situation classique, deux prisonniers. Ici nous choisirons plutôt deux personnes engagées dans une transaction commerciale. À chaque partie, selon les règles du jeu, quand quelqu’un trompe son partenaire, il gagne 5 points alors que celui qui lui a fait confiance « naïvement » ne gagne rien. Quand chaque partenaire trompe l’autre, chacun ne gagne qu’un point. Quand les deux font confiance, alors ils gagnent chacun 3 points.

Lors d’une seule partie, il vous semble logique de tromper car, ce faisant, vous gagnez ou, au pire, faites jeu égal avec votre adversaire : si votre partenaire vous fait confiance, vous gagnez 5 points en le trompant et s’il trahit aussi, vous avez chacun 1 point, mais c’est mieux que d’avoir 0 si l’adversaire vous trompe. Pour que chaque partenaire gagne 3 points en faisant confiance à l’autre, il faut qu’il sorte de sa logique primaire et fasse confiance a priori.

La situation est plus intéressante dans le jeu itéré où chacun joue successivement un grand nombre de parties avec le même partenaire. Le jeu est de faire comprendre au partenaire qu’il vaut mieux que chacun fasse confiance à l’autre pour que vous gagniez chacun trois points à chaque partie. Quand votre partenaire vous trompe à une partie, vous devez l’amener à sortir avec vous du puits commun de la tromperie réciproque. L’avancée de Freeman Dyson et William Press concerne ce jeu itéré où, dans certaines conditions, ils ont mis au point une stratégie gagnante contre toute autre (voir l’article de Jean-Paul Delahaye dans le numéro de janvier 2014 de Pour la Science).

Mais Dyson et Press se trompent partiellement : l’enseignement est que gagner contre un adversaire après un ensemble de parties n’est pas important (la stratégie méchante qui trompe tout le temps gagne ou fait jeu égal avec n’importe quelle autre stratégie), ce qui compte vraiment, c’est de gagner beaucoup de points.

Dans une version du jeu itéré, on fait un pool de nombreuses stratégies qui jouent toutes les unes contre les autres en une succession de tournois (comme dans une compétition darwinienne pour la survie). Il y a, sauf au premier tournoi, plusieurs exemplaires de la même stratégie. À l’issue d’un tournoi, chaque stratégie participante compte ses points et on totalise le nombre de points collectés par les différents exemplaires de chaque stratégie. Ensuite, selon les résultats de ce décompte, l’effectif de chaque stratégie pour le prochain tournoi est ajusté de façon à être proportionnel au nombre de points marqués dans le dernier tournoi. Puis on recommence. On regarde, à la fin de la séquence de tournois, les stratégies qui ont le plus de représentants : ce ne sont jamais les stratégies agressives qui gagnent les tournois, mais celles de type « donnant-donnant ». La stratégie « donnant-donnant » consiste à faire confiance lors du premier coup, puis à jouer au coup n ce que l’adversaire a joué au coup n-1 ; cette stratégie punit celui qui trompe puis fait confiance quand l’autre a recommencé à faire confiance.

Les conclusions de l’étude sont multiples : vous ne ferez pas fortune en trompant toujours vos partenaires, vous pouvez gagner toutes les batailles sans gagner la guerre (la partie gagnée par une tromperie est une victoire à la Pyrrhus), ceux qui deviennent riches permettent aux autres de le devenir aussi, il ne faut pas s’en offusquer, et surtout, il faut faire confiance !

Remarquons enfin un effet de bord. Lors de la dernière partie, vous avez intérêt à tromper l’adversaire, qui ne pourra pas vous punir lors de parties suivantes. Cela modélise bien la technique à suivre lors de transactions commerciales : aucun des partenaires ne doit savoir que c’est la dernière fois que vous interagissez.

Intéressants enseignements du dilemme du prisonnier.

Référence
1 | Press WH, Dyson FJ. Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent. Proceedings of the National Academy of Sciences of the United States of 2012 ;109(26) :10409-13.