Une étrange cuisson
Publié en ligne le 19 juin 2011 - Esprit critique et zététique -par Kamil Fadel
Ce texte est une reprise de l’article publié dans Découverte (la revue du Palais de la découverte) n°366, janvier-février 2010, pages 32-37.
Selon une histoire que l’on peut trouver sur les forums et les blogs d’Internet et qui circule également via le courrier électronique, il serait possible de cuire un œuf à l’aide de deux téléphones portables. Que penser de cette rumeur ? Un canular ?
L’expérience est facile à mettre en œuvre : prenez deux téléphones portables et mettez-les en « communication » à quelques centimètres l’un de l’autre en plaçant un œuf cru entre les deux. Attendez 65 minutes puis vérifiez l’état de l’œuf : il est cuit et dur ! C’est du moins ce que l’on peut trouver sur Internet, ainsi que sur de nombreuses vidéos et variantes de cette expérience. Dans l’une des variantes qui a connu et qui continue de connaître beaucoup de succès depuis juin 2008, on remplace l’œuf par des grains de maïs pour pop-corn. Après quelques secondes seulement de liaison téléphonique entre deux ou plusieurs portables, on voit les graines sauter !
À notre connaissance, la description de l’expérience de la cuisson de l’œuf a été publiée la première fois en anglais sur Internet en 2000 sur le site Wymsey Village Web 1, un site humoristique britannique. Dans leur description du protocole expérimental présenté avec humour, en plus des deux téléphones portables, il fallait aussi… écouter la radio pendant la cuisson ! On peut apprécier l’humour…
Cet article a connu immédiatement un immense succès et demeure à ce jour la page la plus visitée du site. Six ans plus tard, en 2006, le tabloïd russe Komsomolskaya pravda publie un article similaire, présentant des photographies du dispositif expérimental, l’état de l’œuf… Les journalistes Vladimir Lagovski et Andrei Moiseynko indiquent avoir obtenu un œuf dur après 65 minutes de mise en communication des deux téléphones portables. Aussi, en conclusion de leur article, les auteurs déconseillent le port de deux portables dans les poches d’un pantalon !
Qu’en est-il vraiment ? Abordons tout d’abord cette question à travers une analyse de physique élémentaire avant de réaliser cette expérience.
Qu’émettent les portables ?
Comment un portable pourrait-il chauffer un œuf ? Avant de répondre à cette question, voyons comment une lampe peut chauffer de l’eau. Dans la salle d’optique du Palais de la découverte, les visiteurs peuvent observer une expérience de « miroirs ardents » (fig. 1a). Grâce à une lampe de 1 000 W et le montage expérimental dont on peut voir le schéma (fig. 1b), l’eau tiède à 20°C contenue dans un bécher est portée à 80°C en une heure. Comment une telle chose est-elle possible ? D’où vient l’énergie nécessaire pour élever la température ? La réponse est un peu plus subtile que celle que donnent généralement les visiteurs : la lumière bien sûr ! Sans entrer dans trop de détails, et pour faire simple, voici ce que l’on peut dire : le verre et l’eau étant transparents à la lumière, ils ne l’absorbent pas. Par conséquent, en traversant le récipient, la lumière n’y a rien perdu, n’y a pas déposé d’énergie. Ce n’est donc pas la lumière (visible) qui élève la température de l’eau, mais un autre rayonnement. Manifestement, nos yeux ne voient pas ce dernier rayonnement dont l’absorption par le récipient et/ou l’eau permet d’élever la température. Il s’agit du rayonnement infrarouge. Plus de 95 % de l’énergie émise par une lampe à incandescence l’est sous forme de rayons infrarouges.
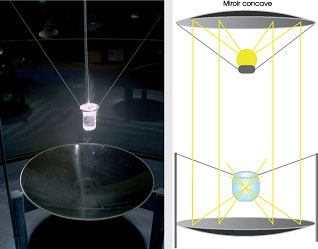
© Palais de la découverte / C. Judei.
Les téléphones portables, quant à eux, n’émettent ni lumière, ni rayons infrarouges, mais un rayonnement micro-onde, de même type donc que celui qui est émis par les fours micro-ondes pour cuire les aliments. Signalons aussi qu’indépendamment des fours et des téléphones portables, la Terre, le système solaire et les galaxies de l’Univers baignent dans un rayonnement micro-onde issu du Big Bang.
Cuire un œuf avec un portable ?
Effectuons de manière approximative un calcul élémentaire permettant d’estimer l’ordre de grandeur de l’énergie qu’il est nécessaire de fournir à un œuf à 5°C sorti du réfrigérateur pour le porter à l’état de cuisson d’un œuf dur. Nous estimerons ensuite l’énergie émise par un portable en 65 minutes. Nous comparerons alors les deux valeurs pour conclure.
Énergie nécessaire à la cuisson
Il ne s’agit pas ici d’effectuer un calcul précis, mais de trouver un ordre de grandeur. Pour cela, nous devons d’abord connaître la température à laquelle un œuf devient dur. Cette valeur peut être estimée, mais elle peut aussi être trouvée dans la littérature : 70°C environ. Il faut donc porter à 70°C un œuf initialement à 5°C, soit une élévation de 65°C. La question à laquelle il faut à présent répondre est celle-ci : combien de joules faut-il fournir à un gramme d’œuf pour élever sa température de 1°C ? Sans doute, à peu de chose près, autant qu’il faut fournir à 1g d’eau pour élever sa température de 1°C. Or, il faut fournir approximativement 4 J pour effectuer une telle opération : 4 joules par gramme par degré. Si l’œuf pèse 60 g, cela exigera 240 J pour élever sa température de 1°C. Pour élever sa température de 65°C, il faudra 65 fois plus d’énergie soit : 65 × 240 = 16 000 J environ.
Énergie émise par un portable en 1 heure
La puissance émise par un portable en fonctionnement normal est d’environ 0,3 J par minute ou 1 200 J en 65 minutes. Comme le rayonnement s’effectue dans toutes les directions, c’est au mieux la moitié des 1 200 joules émis par un portable qui peut atteindre l’œuf, soit 600 J. Avec deux portables, cela fait 1 200 J. Nous sommes loin des 16 000 J nécessaires ! Continuons toutefois le raisonnement pour y voir plus clair…
Température maximale de l’œuf
Même si l’on admet que la totalité des 1 200 J est absorbée par l’œuf, ce qui est fortement improbable, cela permettrait d’augmenter sa température au mieux de 1 200 / 4 / 60 = 5°C seulement. Étant initialement à 5°C, l’œuf passera donc à 10°C. Cela dit, il n’est pas nécessaire d’employer des portables pour porter l’œuf à 10°C. Il suffit de le mettre dans une poche ou le laisser à l’air libre. Une fois sorti du réfrigérateur, il finira de toute façon par être à 10°C et même davantage, à la température ambiante. Même si l’œuf est initialement à la température ambiante, mettons 20°C, soumis au rayonnement des deux téléphones portables, il pourra au mieux atteindre 25°C. « Au mieux », car dès que sa température dépasse les 20°C, étant plus chaud que son environnement, l’œuf se met alors à réchauffer un peu l’environnement plus froid dans lequel il baigne. C’est donc l’environnement qui absorbera en fin de compte une partie de l’énergie émise par les portables. Ces derniers verront leur efficacité de chauffage diminuer.
En résumé, il y aura compétition entre deux effets : d’une part, l’énergie absorbée par l’œuf due aux micro-ondes des portables, toujours égale à 0,3 J par seconde ; d’autre part, l’énergie perdue par l’œuf vers l’environnement plus frais. Cette perte va d’ailleurs croître avec la température de l’œuf. On peut se demander pour quelle température è de l’œuf l’énergie perdue va compenser celle absorbée. Comme à cette température il y aura match nul entre les gains et les pertes, la température de l’œuf ne pourra augmenter davantage et se stabilisera à cette valeur è que nous allons maintenant déterminer.
La température de match nul
Comme indiqué précédemment, l’énergie émise par les portables et absorbée par l’œuf vaut au mieux 0,3 J par seconde, soit une puissance de 0,3 W. Comment l’œuf perd-il de l’énergie vers son environnement plus froid ? Par trois mécanismes : par conduction vers l’air (contact avec l’air frais), par convection (le brassage de l’air qui renouvelle l’air chaud par de l’air frais) et par… rayonnement. En effet, bien qu’il ne nous soit pas possible de communiquer avec notre œuf, ce dernier émet comme tout corps un rayonnement par sa surface en raison de sa température.

© Palais de la découverte / C. Rousselin.
Par exemple, notre propre corps émet de l’énergie principalement dans le domaine des infrarouges dits « moyens » (fig. 2). Concernant notre œuf, intéressons-nous à ses pertes d’énergie par rayonnement. Pour cela, nous devons connaître la loi qui nous donne l’énergie rayonnée par seconde (la puissance) en fonction de la température du corps : c’est la loi de Stefan-Boltzmann, établie expérimentalement par Josef Stefan (1835-1893) en 1879 puis démontrée théoriquement par son élève Ludwig Boltzmann (1844-1906) en 1884. Strictement parlant, elle ne s’applique qu’au rayonnement émis par un corps idéal que les physiciens désignent par « corps noir ». Cependant, dans le contexte qui nous préoccupe où nous nous intéressons à des ordres de grandeur, nous appliquerons la loi de Stefan-Boltzmann à l’œuf, bien qu’il ne soit pas tout à fait un corps noir idéal. La loi de Stefan-Boltzmann dit que l’énergie P rayonnée par seconde (la puissance en watt), est proportionnelle à la surface S du corps et à la puissance quatrième de sa température T (prise en kelvin). Le coefficient de proportionnalité, appelé coefficient de Stefan-Boltzmann, est noté σ :

Supposons tout d’abord qu’à la sortie du réfrigérateur, l’œuf soit simplement placé dans un environnement à 20°C, sans aucun portable. En vertu de la loi de Stefan-Boltzmann, l’œuf va rayonner à 5°C (278 K). Il va aussi recevoir un rayonnement de la part de son environnement assimilé à un corps noir à 20°C (293 K). Il recevra donc davantage de rayonnement qu’il n’en émettra : sa température pourra grimper avant de s’équilibrer avec celle de l’environnement. Calculons la puissance reçue par l’œuf de son environnement. Si l’on estime la surface S de l’œuf de 60 g à 75 cm2, la puissance reçue par l’œuf est donnée en multipliant 5,67.10-8 par 75.10-4 (surface de l’œuf en m2) et par 2934. Cela donne 3,13 W. Ce chiffre est à comparer au 0,3 W fourni par les portables. L’environnement à 20 °C chauffe donc l’œuf bien plus que ne le font les portables ! Lorsque la température de l’œuf atteint 20°C, ce dernier émet une puissance de 3,13 W vers l’environnement et en reçoit 3,13 W également : sa température ne change plus ; il y a équilibre thermique. Installons alors les deux portables et admettons qu’ils feront passer la puissance totale reçue par l’œuf à 3,13 + 0,30 = 3,43 W. À présent, la question consiste à déterminer la température ϴ à laquelle l’œuf émettra 3,43 W. En effet, si l’œuf rayonne 3,43 W, c’est-à-dire autant qu’il reçoit, sa température ne pourra plus augmenter. Le calcul donne
soit une élévation de température de 7 °C environ. La température de l’œuf ne pourra ainsi jamais dépasser 27 °C, même en laissant les portables en communication pendant des journées entières. Pour chauffer l’œuf, mieux vaut donc le couver dans la main… Rappelons ici que nous avons abouti à ce résultat en ayant omis de prendre en compte le rafraîchissement de l’œuf par conduction et convection. Plus important : nous avons posé comme hypothèse que la totalité des 1 200 J était absorbée par l’œuf, une hypothèse peu raisonnable mais qui nous a permis de montrer que l’élévation de température ne peut en aucun cas être supérieure à 7 °C. Dans la pratique, l’élévation de température de l’œuf sera donc en fait très inférieure à cette valeur. De manière générale, on connaît souvent très bien les puissances émises, en revanche les puissances absorbées sont beaucoup moins bien connues et difficiles à évaluer, surtout lorsqu’il s’agit du vivant.
Expérience
Nous avons réalisé l’expérience suivante (fig. 3 a, b, c, d) : placé dans une pièce à 23°C, et coincé entre deux portables en communication, l’œuf, initialement à 23,5 °C, est passé à 23 °C après 65 minutes. C’est donc bien l’environnement qui impose la température de l’œuf et non les portables.

Figure 3a.
Nous avons commencé par prendre la température de l’œuf en y insérant une fine sonde thermique à travers un petit trou réalisé dans la coquille de l’œuf.
|

Figure 3b.
Après quoi, nous avons installé de part et d’autre de l’œuf deux téléphones portables qui sont restés en communication pendant plus de 1 heure.
|

Figure 3c.
Après 65 minutes, nous avons mesuré de nouveau la température de l’œuf. Elle s’était équilibrée avec celle de la salle à 23°C : c’est la salle qui impose la température et non les portables.
|

Figure 3d.
Enfin, nous avons brisé l’œuf afin de ne laisser aucun doute sur l’état cru de l’œuf.
|
Qu’en est-il des pop-corn ?
La préparation de pop-corn nécessite le chauffage du maïs, plus précisé-ment de la variété Butterfly, à… 180°C. Il est par conséquent tout à fait impossible de préparer du pop-corn avec des portables. Les vidéos que l’on peut voir sur Internet sont toutes des trucages. Il s’agit soit de trucage numérique de vidéo ; soit de la dissimulation d’un dispositif de chauffage (plaque chauffante ou émetteur micro-ondes de four) à proximité immédiate des pop-corn, le plus souvent sous la table…
Quoi qu’il en soit, si un portable était en mesure de chauffer un œuf à 70°C et le pop-corn à 180°C, cela se remarquerait par un échauffement important de la main et de l’oreille lors d’une communication prolongée, ce qui n’est manifestement pas le cas…
Merci à Jacques Treiner pour ses remarques, suggestions et sa participation à la réalisation de l’expérience avec les portables.
1 https://web.archive.org/web/2001021... (disponible sur archive.org—27janv.2020)
Publié dans le n° 294 de la revue
Partager cet article
Esprit critique et zététique

Une fausseté répétée mille fois
Le 17 avril 2019
Evidence Based Bonne Humeur… à la poursuite de l’esprit critique
Le 6 février 2024
Souvenirs, souvenirs
Le 2 février 2024
Esprit critique SPS 346
Le 29 janvier 2024
Entretien avec Luc Rodet
Le 16 janvier 2024